Python Lab 1

Part C: Methods for Local Optimization

Part C-1: The Lennard-Jones Potential

One of the simplest and most widely used potentials for describing the interaction between two atoms is the Lennard-Jones(L-J) potential:

V_LJ(r) = 4 ε [ (σ / r)¹² - (σ / r)⁶ ]
In the equations above, σ and ε are free parameters that can be tuned to the molecular system being modeled. Below are a few simple exercises to further understand the L-J potential.

1. First, you will need to copy over a directory with the starting python scripts for this assignment. Copy this directory by typing cp -r /home/fri/lab_files_2022/lab1_part_c . Then, go into this directory.
   
   
2. In this directory is a script called lj_1d.py. This script produces a plot called 'LJ_s1_e1.png', which plots how the L-J potential changes with bond length for σ = 1.0 and ε = 1.0. Run this script by typing ./lj_1d.py . Now you can view the figure you produced by typing eog LJ_s1_e1.png .
   
   Note: this script includes a new module called matplotlib which is used for creating plots. You can checkout this tutorial to learn more.
   
   
3. Try making the following changes the parameters σ and ε and plot the LJ potential. Save the images of the various plots you make for Question 2 below (you will want to save the figure name to save all .png files). Also, adjust the range in the y-axis of these plots to fit the parameters selected.
   
   
   • σ = 1. and ε = 5.
   • σ = 5. and ε = 1.
   • σ = 5. and ε = 5.
   
   How does σ and ε change the L-J potential? You will need to answer this in Question 2 at the end of this assignment and use the figures created to support your answer.
   
   

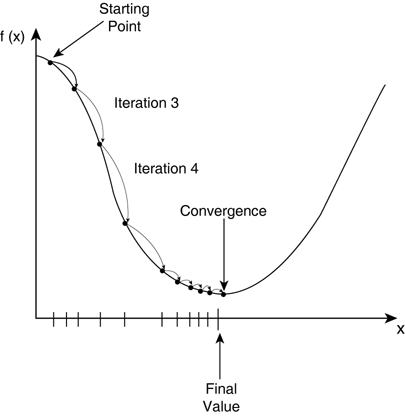
Part C-2: Gradient Descent Method

The next part of this lab will walk you through implementing your first method for local optimization: gradient descent (i.e. steepest descent).

1. Find the optimal distance between two atoms in the L-J potential (σ = 1.0 and ε = 1.0) analytically. Do this using pen and paper with a 1D system like the L-J potential. Recall that the optimal distance is a local minimum or a critical point on the potential energy surface.
   
   
2. The next steps will guide you through finding the optimal distance between two atoms in the L-J potential numerically using the gradient descent method. Recall that in the gradient descent method you follow the force or the direction of steepest descent toward a local minimum:
   r_n+1= r_n + α F(r_n)
   where r_n is the position of the atoms after n steps, F is the force, and α is a free parameter. You will make the following edits to the script lj_1d.py:
   
   
   1. Create a function called force which takes one variable, r (the bondlength) and that returns the force for the LJ potential at r for epsilon = 1.0 and sigma = 1.0. (We will use these values of σ and ε for the remainder of the assignment). This function will be used to calculate the force in the next step of this assignment.
      
      
   2. Create a function called gradient_descent which takes three variables, r, alpha, and convergence_criteria. Then create a while loop that repeats the following equation until the magnitude of the force is less than the parameter convergence_criteria:
      r_n+1= r_n + α F(r_n)
      Add a line(s) to your while loop where you print the potential energy, bondlength and force. This will give you feedback for the debugging process.
      For example: if your force is not dropping consistently, or that your energy is not dropping consistently, you may but not necessarily have a bug because the gradient descend method is supposed to produce a trajectory with decreasing force and energy.
      
      
   3. Call the gradient_descent function with the variables r = 1.05, alpha = 0.005, and convergence_criteria = 0.01. You should find the same result that you found analytically. Once you find the same result, your optimizer is working, at least for this initial position!
      
      Note: there are normally bugs in code! Check out this page for tips. Try writing out pseudocode to make sure your code matches your intended logic. You can also use the information you are printing to see what is going wrong. For example, what do you expect to happen to the potential energy as you iterate through the gradient descent algorithm?
   
   
   
3. Next, we will plot the trajectory of your optimizer at different initial values of r and values of α. Specifically you will plot how r_n, F(r_n), and V(r_n) changes over the step number,n. To do this, we will need to edit and create a few functions:
   
   
   1. First edit your gradient_descent function so that it creates and returns five arrays containing the step number, force vector, force magnitude, potential energy, and bondlength throughout these trajectories.
      
      
   2. Then create a function called plot_trajectory (similar to plot_pes) which takes the step number array, one other array (r, V, F, or magF) and any other variables needed to label your plot. This function should produce a plot of the step number (x-axis) versus another variable (r,V or F).
      
      
   3. To test these two functions, produce plots of how the bondlength, force and potential energy changes throughout the optimization for the parameters from the previous question.
      
      
   4. Note: You will produce a lot of graphs in this exercise. You can change the figure names with the function savefig in your script. I would suggest creating a logical naming scheme. Note that you should not have spaces in the file names you select for your figure (i.e use "Nvmagforce_alpha0.1.png" not "N v magforce alpha 0.1.png").
   
   
   
4. Next, set the initial value of r to 0.95. Does your code reach the correct local minimum? If not, you have a bug. Either way, make all three plots for this new initial condition. These plots may help with the debugging process. If you have a bug, find it!
   
   
5. Change α to a value higher and lower than 0.005 by atleast two orders of magnitude and make the same plots as listed above. Use r equal to 0.95 and the same convergence criteria.
   
   
6. As you create the graphs above, consider α's role in gradient descent:
   
   
   • How many steps did your optimizer take?
   • Did it find the correct solution?
   
   

Questions for Part 2

Post all answers to a word document like Google Docs or Microsoft Word.

1. In the Lennard-Jones potential, how do the parameters ε and σ effect the potential energy surface? Include plots of the PES to explain your answer.
2. What is the optimal distance between two atoms in the L-J potential (ε = 1.0 and σ = 1.0)? Type the equation you solved to find this answer analytically.
3. What are the pros and cons of high and low values of α? What values did you select? To explain this include plots of how the bond length, force, and potential energy changed over optimization step number for various values of α. Be sure to label your axes! This question will be worth atleast twice as many points as the previous questions!